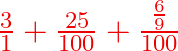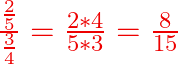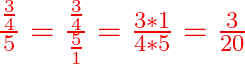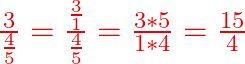LeCoinAtelier.com

Des tutos sur les usinages mécaniques

LeCoinAtelier.com

Auteur/autrice : Pierre-André Montandon

Le filetage au tour

de

Le 13 avril 2023

dans Tournage

Le filetage au tour, permet de réaliser des vis pour lesquelles nous n’aurions pas de filières ou de tarauds adaptés. Il peut aussi être utilisé lorsque l’on veut une vis de grande précision.

Présentation

Pour réaliser cela, vous avez besoin d’un système de filetage avec une vis mère qui entraine le burin de filetage. Il existe plusieurs systèmes différents. Sur certain tour c’est le chariot du tour qui se déplace. Dans ce cas, la vis mère peut-être celle du chariot supérieur ou petit chariot. Dans d’autre cas, c’est le trainard qui est relié à la vis mère.

Un autre système de filetage au tour existe, comme le mien par exemple qui comporte une patronne (vis mère) et un peigne qui entraine un chariot spécial pour le filetage. Ce système se retrouve principalement sur les tours Schaublin 102.

Dans tous les cas, vous aurez encore besoin d’un train d’engrenage qui lie la broche du tour et la vis mère. On calculera ce train en fonction du pas que l’on veut réaliser et du sens de filetage (gauche ou droite).

Cette opération peut paraître compliquée à calculer, mais en fait ce n’est pas si difficile que cela. Sans entrer dans un détail mathématique compliqué, je vais vous montrer comment on fait. Ensuite on réalisera aussi en même temps une pièce filetée.

Calcul du rapport de pas

Pour commencer un filetage au tour, il faut avant toute chose connaitre le pas de la vis qu’on veut réaliser et le mettre en fraction (tuto sur les fractions ici). On appellera ce pas P1.

Exemples :

si la vis à réaliser a un pas de 2 mm alors : P1 sera 2

Si la vis à réaliser a un pas de 1.5 mm, alors : P1 sera  \frac{15}{10}=\frac{3}{2}

Si la vis à réaliser a un pas de 1.\overline{6} mm, alors : Pour mettre en fraction une valeur périodique, c’est très simple. On prend tous les chiffres de la période que l’on met en haut de la fraction (dividende) et on met en bas de la fraction (diviseur) autant de 9 qu’il y a de chiffre dans la période donc pour nous :

P1 sera \frac{1}{1}+\frac{6}{9}=\frac{1}{1}+\frac{2}{3} . En mettant au même dénominateur commun on a : \frac{3}{3}+\frac{2}{3} qui s’écrit aussi \frac{3+2}{3}=\frac{5}{3}.

Ensuite il faut connaitre le pas de la vis mère (celle qui entraine le burin) qu’on appellera P2. Selon les systèmes, on dispose de plusieurs vis mères avec des pas différents.

La formule à appliquer est : \frac{P_1}{P_2} . C’est en fait le rapport qu’il y a entre le nombre de tour de la broche et le nombre de tour de la vis mère. Donc si j’ai une vis mère avec un pas de 2 mm, on aura selon mes exemples précédents pour :

P1 = 2 mm ==> \frac{P_1}{P_2}=\frac{2}{2} = 1 tour de vis mère pour un tour de broche.

P1 = \frac{3}{2} mm ==> \frac{P_1}{P_2}=\frac{\frac{3}{2}}{2}=\frac{3}{2*2} =\frac{3}{4}  tour de vis mère pour un tour de broche.

P1 = \frac{5}{3} mm ==>\frac{P_1}{P_2}=\frac{\frac{5}{3}}{2}=\frac{5}{3*2} =\frac{5}{6} tour de vis mère pour un tour de broche.

Choix des engrenages

Il reste maintenant à déterminer le rapport d’engrenage qui correspond à cette fraction. Vous trouverez ici,  un tuto sur le calcul des rapports d’engrenage. Je ne vais donc pas m’attarder à cela ici. Toutefois, il est important avant de partir dans le rapport d’engrenage, de connaitre dans quel sens va tourner votre pièce et votre vis mère. Si votre filetage est dans le même sens que la vis mère (droite ou gauche), alors la vis mère tournera dans le même sens que votre pièce, sinon elle tournera dans l’autre sens.

Si vous disposez de plusieurs vis mères, il vous faudra réaliser toutes ces opérations pour chaque vis mère que vous avez. Si aucune solution n’est possible, alors il faut acheter ou fabriquer d’autres engrenages.

Une dernière petite chose importante avant de vous lancer. Si vous disposez d’un système débrayable comme le mien, il faudra faire attention de ne surtout pas débrayer entre les passes, lorsque le pas que vous réalisez n’est pas un diviseur du pas de la vis mère. En d’autre terme, si vous divisez le pas de la vis mère, par le pas à fileter et que le résultat n’est pas un nombre entier, alors ne pas débrayer, sinon on risque de ne pas se retrouver dans le bon pas. En pratique si vous avez plusieurs vis mère et que votre système est débrayable, vous choisirez de préférence, une vis mère qui est un multiple du pas à fileter. Si vous ne débrayez pas, il faudra absolument dégager le burin lors du retour, afin de permettre le rattrapage du jeu qu’il y a dans la vis et les engrenages.

Montage des roues

Voilà, maintenant passons à la pratique. Je dois réaliser une vis M33 x 2.00. J’ai une vis mère avec un pas de 2mm. Je vais donc partir sur mon premier exemple pour le montage des roues.

Photo du montage des roues pour un rapport 1, dans le cas du filetage au tour.
Montage des roues rapport 1

Sur mon système, la première roue solidaire de la broche comporte 50 dents. Donc j’ai monté la dernière roue (celle solidaire de la vis mère), une roue de 50 dents. Entre deux, c’est uniquement de la transmission et inversion de sens. On voit que j’ai aussi utilisé deux roues qui n’engrènent avec rien. Elles sont là uniquement comme entretoises.

Montage du système de filetage

Avant de fileter, il est nécessaire de connaître l’angle d’inclinaison de l’hélice du filetage, afin d’incliner notre burin de la bonne valeur. Lorsque l’on dessine un profil de pas, il est en fait en coupe perpendiculaire au filet. Donc notre burin qui a la même forme que le profil dessiné, doit être incliné pour respecter ce profil. Vous trouverez la formule pour calculer cet angle dans le pdf suivant, ainsi que la formule pour calculer la profondeur du pas. Ces formules sont pour un pas métrique.

Pdf profile pas M33x2.00

La mesure sur pige (M) que vous avez trouvée dans le pdf, peut vous être utile, si vous réalisez une vis et que vous n’avez pas l’écrou pour tester votre filetage. Vous pouvez prendre un morceau de matière de votre stock, que vous mesurez précisément et vous faite le calcul avec ce diamètre de piges. Si vous le faites comme cela, avec des piges à tenir dans la main, vous avez meilleures temps d’en prendre que deux.

Je vais maintenant monter la vis mère et préparer le chariot de filetage. Dans la vidéo qui suit, vous verrez le système par peigne et patronne qui est présent sur bons nombres de tours Schaublin 102.

Passons maintenant aux derniers réglages.

On est maintenant prêt à fileter. Je mets personnellement toujours, quel que soit le diamètre, la plus petite vitesse de rotation et j’adapte mes profondeurs de passes en fonction.

Réalisation

En résumer, ce qu’il faut comprendre du filetage au tour, c’est que ça dépanne très bien, mais que c’est relativement long à mettre en place. En tout cas pour le système par peigne et patronne. Par contre ce système à l’avantage d’avoir plusieurs vis mères interchangeables. Tous les systèmes nous permettent de réaliser n’importe quel pas, pour autant que l’on dispose des bonnes roues dentées.

J’espère que cela vous a permit d’y voir un peu plus claire sur le filetage au tour. N’hésitez pas à laisser vos commentaires en dessous.

A bientôt

PAM

Retrouvez également toutes mes vidéos sur ma chaine YouTube.

Tous les Articles

Les manipulations de fractions

de

Le 22 mars 2023

dans Général

Dans ce tuto, j’essaye d’expliquer la mise en fraction et les manipulations de fractions principales. J’essaye surtout d’amener des solutions toutes prêtes, sans passer par trop de bla bla pour justifier ce que je dis.

Je reviendrai sans doute sur ce tuto par la suite, mais n’hésitez pas à laisser vos commentaires et suggestions en bas.

La mise en fraction d’un nombre décimal.

Exemple 15.678

15 est la partie entière et 678 est la partie décimale.

La partie entière se met en fraction \frac{}{1}. Donc ici \frac{15}{1} . A cela on ajoute (l’addition de fraction est vue plus bas) la fraction de la partie décimale. Si on a une décimale, ce sera des \frac{}{10}, si on a deux décimales, ce sera des \frac{}{100}, si on a 3 décimales, ce sera des \frac{}{1000}, etc. On met le chiffre 1 suivit d’autant de 0 qu’il y a de chiffre dans la décimale. Dans cet exemple, ce sera \frac{678}{1000}.

Donc pour notre exemple on écrira :

\frac{15}{1}+\frac{678}{1000}

Si ce nombre décimal, comporte une valeur périodique,

Exemple 1.\overline{345}

Alors on prend les chiffres de la période et on les divise par autant de 9 qu’il y a de chiffre. Pour nous ici, ce sera \frac{345}{999}. Donc dans cet exemple la mise en fraction est :

\frac{1}{1}+\frac{345}{999}

Il peut aussi arriver que la partie décimale soit avec une partie fixe et une partie périodique.

Exemple 3.25\overline{6}

Dans ce cas on met la partie fixe comme vu plus haut, pour nous ici ce sera \frac{25}{100} et on y ajoute \frac{\frac{6}{9}}{100}.

Donc on aura :

\frac{3}{1}+\frac{25}{100}+\frac{\frac{6}{9}}{100}

Si le 6 périodique était en 2ème position on aurait eu \frac{\frac{6}{9}}{10} et si il était en  4ème position on aurait eu \frac{\frac{6}{9}}{1000}.

L’amplification et la réduction de fraction

L’amplification consiste à multiplier le diviseur et le dividende par le même nombre.

Exemple : J’amplifie \frac{1}{3} par 4.

\frac{1}{3}=\frac{1*4}{3*4}=\frac{4}{12}

La réduction de fraction est l’opération inverse. C’est à dire qu’on divise le dividende et le diviseur par le plus grand diviseur commun. Donc dans notre exemple, on peut diviser le haut par 4 et le bas par 4 et on retrouve notre \frac{1}{3} qui n’est pas réductible.

La réduction de fraction peut des fois être fastidieuse, lorsque l’on a des grands nombres. C’est pour cela que j’ai mis, ici, un outil qui réduits les fractions.

Cependant on n’a pas toujours accès à ces outils informatique. Une méthode assez rapide pour trouver le plus grand diviseur commun est d’effectuer la division euclidienne (entière) et ensuite de diviser le diviseur par le reste et ainsi de suite jusqu’à avoir un reste égal à 0. Le plus grand diviseur commun est alors le dernier diviseur.

Exemple : \frac{5196}{6495}

Méthode de détermination du plus grand diviseur commun avec la division euclidienne. Pour les manipulations de fraction

Le plus grand diviseur commun est donc 1299. Ce qui donne : 5196/1299 = 4 et 6495/1299 = 5

\frac{5196}{6495}=\frac{4}{5}

Attention, l’amplification et la réduction de fraction n’est pas une multiplication respectivement une division de fraction. On verra cela plus bas.

L’addition ou la soustraction de fraction

Il faut tout mettre au même dénominateur commun. C’est à dire qu’il faut avoir toutes les fractions qui ont le même diviseur. On va donc amplifier les fractions et additionner seulement le haut (dividende).

Exemple : \frac{15}{1}+\frac{678}{1000} ça nous donne :

\frac{15000}{1000}+\frac{678}{1000}=\frac{15000+678}{1000}=\frac{15678}{1000}

On va ensuite réduire cette nouvelle fraction et on obtient.

\frac{15678}{1000}=\frac{7839}{500}

Pour la soustraction c’est la même chose, mais ou soustrait au lieu d’additionner.

La multiplication de fraction

Cette opération consiste à multiplier tous les dividendes entre eux et tous les diviseurs entre eux.

Exemple : \frac{3}{4}*\frac{6}{5}

Cela revient au même d’écrire :

\frac{3*6}{4*5}=\frac{18}{20}=\frac{9}{10}

Si on multiplie une fraction par un nombre entier, alors ce nombre entier est aussi \frac{}{1}. Donc on multipliera le haut par le nombre entier et le bas par 1.

La division de fraction

Exemple : \frac{\frac{2}{5}}{\frac{3}{4}}

On va prendre le dividende de la fraction du haut et le multiplier par le diviseur de la fraction du bas. Cela deviendra notre nouveau dividende et ensuite on prend le diviseur de la fraction du haut et on le multiplie par le dividende de la fraction du bas et ça devient notre nouveau diviseur. Ceci nous donne donc

\frac{\frac{2}{5}}{\frac{3}{4}}=\frac{2*4}{5*3}=\frac{8}{15}

Exemple : \frac{\frac{3}{4}}{5}

5 c’est aussi \frac{5}{1} donc

\frac{\frac{3}{4}}{5}=\frac{\frac{3}{4}}{\frac{5}{1}}=\frac{3*1}{4*5}=\frac{3}{20}

Exemple : \frac{3}{\frac{4}{5}}

3 étant aussi \frac{3}{1} donc

\frac{3}{\frac{4}{5}}=\frac{\frac{3}{1}}{\frac{4}{5}}=\frac{3*5}{1*4}=\frac{15}{4}

Dans ces deux derniers exemple, on voit qu’il faut faire attention où se trouve le nombre entier. En haut de la fraction principale ou en bas ?

Je reviendrai certainement sur ce tuto concernant les manipulations de fractions, par la suite pour l’améliorer. N’hésitez pas à commenter et me donner d’autres idées.

A bientôt

PAM

Retrouvez également toutes mes vidéos sur ma chaine YouTube.

Tous les Articles

La réduction de fraction

de

Le 22 mars 2023

dans Outils

Entrer une fraction et cliquer sur réduire







est aussi égal à

+

Le diviseur

de

Le 11 mars 2023

dans Fraisage

On se sert d’un diviseur, lorsque l’on veut faire des usinages sur le pourtour d’une pièce ronde, ou répartit autour d’un cercle, selon des angles précis. Par exemple pour fraiser un six pans sur une vis que l’on aurait fabriqué, ou réaliser des perçages selon un certain angle donné. On peut aussi l’utiliser pour contourner une pièce de forme, mais toujours en rapport au centre du diviseur. Il divise donc un cercle en angles.

Voici ce que je traite dans ce tuto. Bonne lecture et n’hésitez pas à mettre un commentaire en bas de page.

Le diviseur monté sur la table de la fraiseuse.
Diviseur
Différences entre universel et semi universel

Il existe deux types de diviseurs. Le diviseur semi universel et le diviseur universel. Les deux fonctionnent de manière identique avec quelques petits avantages, non négligeables pour l’universel.

En tournant la manivelle on fait pivoter la broche du diviseur, et le disque à trous nous permet de nous positionner précisément à l’angle désiré. Dans le diviseur semi universel, on est limité pour les angles désirés, aux disques à trous que nous avons. Concrètement, les angles ou rapports d’angle qui donnent une répartition en relation avec des nombres premiers…il faut les oublier. Mis à part les nombres premiers en dessous de 47 (valeur qui peut varier en fonction des disques que l’on a).

Avec le diviseur universel, qui fonctionne de la même manière que le semi universel, nous avons en plus, une boite à engrenage, qui permet entre autre, de corriger les erreurs du semi universel dans ces cas particuliers, donc de réaliser TOUS les angles voulus. Elle permet aussi, dans une autre application, de lier le diviseur à une vis mère, pour le fraisage d’une hélice par exemple.

Je ne m’attarderai pas sur le diviseur universel, car je n’en possède pas, mais pour ceux qui le désirent, j’ai réalisé un tuto sur le calcul des trains d’engrenage, ici. En pilotage d’une vis mère, c’est le même calcul que pour le filetage au tour dont vous trouverez ici, un tuto.

Présentation des principales pièces du diviseur.

La manivelle avec son pointeau.

La manivelle du diviseur.
La manivelle avec le pointeau
La manivelle complète avec le disque à trou et l'alidade monté dessus. Pour le diviseur
La manivelle complète avec vis sans fin

La vis sans fin engrène avec une roue à vis sans fin qui est solidaire de la broche. Donc lorsque l’on tourne la manivelle, on fait tourner la broche selon un rapport qui en général est de \frac{40}{1}. 40 tours de manivelle font tourner la broche de 1 tour. Le pointeau sert à positionner et maintenir, la manivelle dans un des trous du disque à trou.

Les disques à trou.

Les disques à trous. Pour le diviseur
Disques à trou

Ces disques ont plusieurs rangées de trou répartis en divisions égales. Chaque rangée comporte un nombre différent de trou. On choisira le bon disque et la bonne rangée de trou selon le calcul que l’on verra après.

L’alidade.

L'alidade. Pour le diviseur
Alidade

L’alidade sert à positionner la manivelle à la bonne place en fonction du nombre d’intervalles que l’on aura calculé.

Les formules de calcul

Vous avez vu qu’il faut faire quelques calcul avant l’utilisation du diviseur. Passons donc à cela avant la mise en place.

On a besoin de connaitre le rapport entre la manivelle et la broche. On appellera ce rapport « K ».

En générale ce rapport est de 40. Si vous ne le connaissez pas, il suffit une fois, de compter le nombre de tour de manivelle que vous faites pour faire un tour de broche.

Ensuite, soit vous répartissez un nombre de division à effectuer sur 360° et là, on appellera cela « N », soit vous travaillez avec un angle et là on appellera cela « α ». α est aussi égal à \frac{360°}{N}.

Vous avez une formule qui est la suivante :

J’appellerai « x » le nombre de tour de manivelle que je dois faire pour réaliser mes divisions où mes angles.

La formule :

x=\frac{K*\alpha}{360}=\frac{K}{N}=\frac{a}{b}

«\frac{a}{b}» étant le résultat réduit de la fraction.

Comme la manivelle doit faire un nombre de fraction de tour, on effectuera la division entière et on mettra en fraction le reste. Cela nous donne donc avec « q » qui est le contient (partie entière de la division) :

x=q+\frac{a-q*b}{b}

«a-q*b» étant le reste.

q est en fait le nombre de tour entier de la manivelle auquel on ajoute une fraction de tour. Et c’est là que l’alidade nous sera utile.

Calcul avec un nombre de divisions

Je dois réaliser une roue dentée qui comporte 35 dents. Ce sera donc une répartition de :

x=\frac{K}{N}=\frac{40}{35}=\frac{8}{7}

et

x=q+\frac{a-q*b}{b}=1+\frac{8-1*7}{7}=1+\frac{1}{7}

La manivelle fera donc 1 tour complet, plus \frac{1}{7} de tour.

Je dois maintenant amplifier ma fraction de façon à trouver un disque qui a un nombre de trou qui est un multiple du diviseur, donc dans mon cas un multiple de 7. J’inscris donc sur un papier la fraction suivante :

x=1+\frac{1}{7}=1+\frac{~~~}{~~~}

Je possède un disque à 42 trous. C’est parfait. Pour arriver à 42, je multiplie 7 par 6. Ce qui veut dire que je dois aussi multiplier 1 par 6 et j’arrive à :

x=1+\frac{1}{7}=1+\frac{6}{42}

on ferra donc 1 tour entier de manivelle + 6 espaces sur le disque de 42 trous.

Je monte donc le disque qui a 42 trous, je règle le pointeau de la manivelle sur la rangée de 42. Je place ensuite mon alidade contre le pointeau et je compte 6 espaces ou 6 trous, en sachant que le trou ou je me trouve est le trou 0, et je règle l’autre partie de l’alidade juste après cet intervalle en bloquant l’alidade. Pour l’usinage de chaque dent, je devrai faire 1 tour de manivelle, plus l’espace que j’ai entre mon alidade. Après chaque déplacement, je reviendrai appuyer l’alidade contre le pointeau de la manivelle. Vous pouvez voir tous cela (sans l’usinage) dans la vidéo suivante.

En faisant cette manipulation 35 fois, j’aurai au final fait 40 tours entiers de manivelle, donc un tour de broche.

Calcul avec un angle

Je dois fraiser ou percer deux trous selon un angle de 15°. Ce sera donc la formule :

x=\frac{K*\alpha}{360}=\frac{40*15}{360}=\frac{600}{360}=\frac{5}{3}

et

x=q+\frac{a-q*b}{b}=1+\frac{5-1*3}{3}=1+\frac{2}{3}=1+\frac{18}{27}

En prenant le disque de 27 trous, on fera donc avec la manivelle, 1 tour + 18 espaces et on aura réalisé un angle de 15 degrés.

Attention toutefois avec les angles qui ne sont pas des chiffres rond. Il faudra mettre l’angle avec la partie décimale, en fraction (comme je le montre ici, dans le tuto sur les fractions) et si c’est un angle en degrés, minutes, il faudra tout mettre en minutes et y compris les 360. Si c’est avec des secondes, on convertira le tout en secondes ainsi que les 360.

Conclusion

En finalité, c’est le truc qui reste la bête noir de tout apprenti (dont j’ai fait partie) et qui parait insurmontable. Cela reste juste de la manipulation de fraction (des maths oui, oui), mais ça vaut la peine de s’y plonger, car c’est fou ce que l’on peut faire avec un diviseur… J’ai ébauché un tuto sur les fractions et manipulation de celles-ci, ici, et je vous mets en lien ici, un outil qui vous permettra de réduire vos fractions sans vous prendre la tête.

J’espère avoir aidé bon nombre d’entre vous dans l’utilisation du diviseur. N’hésitez pas à laisser vos commentaires en dessous.

A bientôt

PAM

Retrouvez également toutes mes vidéos sur ma chaine YouTube.

Tous les Articles

Le tournage entre pointes

de

Le 4 mars 2023

dans Tournage

Le tournage entre pointes consiste à usiner ou rectifier une pièce qui est serrée entre une pointe dite « fixe » qui tourne avec la broche et une pointe dite « tournante », qui est placée dans la contre poupée et qui est entrainée par la pièce. Pour empêcher la pièce de glisser sur les pointes, on utilise un plateau qui entraine le toc et la pièce.

Présentation
Montage d'une pièce entre pointes avec le plateau et le toc.

Cette opération est principalement utilisée pour du rectifiage qui nécessite une concentricité quasi parfaite d’un bout à l’autre de la pièce et ce, même après retournement. On peut aussi l’utiliser pour tourner des pièces parfaitement concentriques. Je l’utilise aussi pour des pièces que je ne peux pas serrer dans un mandrin, du fait de leur géométrie. C’est ce dernier cas de figure que j’utilise dans la vidéo ci-dessous.

Comme indiqué précédemment, on utilise donc :

  • Un plateau avec doigt, tournant avec la broche du tour
Plateau tournant avec doigt. Pour le le tournage entre pointes
Plateau tournant
  • Un toc entrainant la pièce (celui de la photo est un toc maison, dont vous pourrez trouver le dossier technique en téléchargement dans quelques jours.
Toc d'entrainement. Pour le le tournage entre pointes
Toc
  • Une pointe fixe (celle de gauche) placée dans la broche du tour et une pointe tournante (celle de droite) placée dans la contre poupée.
Pointe fixe et pointes tournante. Pour le le tournage entre pointes
Pointes
Méthode

Avant de pouvoir usiner la pièce, il est nécessaire d’y faire un centrage des deux côtés à l’aide d’une mèche à centrer. Petit rappel concernant la mèche à centrer. Il faut impérativement forer le trou jusqu`au cône de 60° et y compris une partie de celui-ci (cône qui se termine sur le corps de la mèche) voir photo ci-après, sinon les pointes ne toucheront pas correctement la pièce.

Schéma de centrage sur une mèche à centrer.

Une fois cela réalisé, placez le toc d’un côté de la pièce et serrez le. Réglez le doigt afin qu’il entraine le toc, mettez en contact le doigt et le toc (ceci pour éviter un choc lorsque le doigt se mettra en mouvement) et enclenchez le tour. Vous pouvez dès lors usiner la pièce. Vous pouvez à tout moment retourner la pièce pour usiner l’autre côté sans que cela ne pose de problème de concentricité. N’oubliez pas de lubrifier la pointe tournante afin de la préserver d’un grippage.

Le toc, une fois serré sur une portée ronde, peut avoir tendance à glisser si la force d’usinage est trop grande. Il faut donc adapter ses passes et la vitesse d’avance en conséquence.

En usinage d’ébauche, il est préférable d’ébaucher tout ce que l’on peut en mandrin ou en pince et ensuite seulement réaliser la finition entre pointe. Exactement comme si vous ébauchiez une pièce à tremper et que vous faisiez le rectifiage après trempe, entre pointes.

Réalisation

Je vous mets ci-après un petit montage (vidéo et photo) de l’usinage de la pièce que j’ai réalisé entre pointes.

Pour information cette pièce est un outillage que j’ai fait pour ma presse à balancier. Malgré certaines contraintes de forme tolérancées, j’aurais très bien pu l’usiner en la serrant au départ sur un mandrin 4 morts indépendants. Ceci dit, tout le monde ne possède pas ce genre de mandrin et cette solution s’avère être bien pratique. Le mieux encore aurait été de partir d’une barre ronde, mais je n’en avais pas en stock. Pendant l’usinage de cette pièce, je me suis rendu compte d’une chose. Une fois l’ébauche réalisée sur un côté, j’aurais dû faire le reste de l’ébauche en mandrin puis revenir au tournage entre pointes pour la finition. C’est quand même allé, mais j’ai pas mal galéré.

Ce qu’il faut retenir de ce mode d’entrainement. Cela permet de travailler sur toute la longueur de la pièce, en gardant une concentricité parfaite. Par contre ce système ne permet pas d’entrainement avec de gros efforts, on l’utilisera prioritairement pour les passes de finition.

Voilà c’est à peu près tout ce que j’avais à présenter sur le tournage entre pointes. N’hésitez pas à laisser vos commentaires et/ou question en dessous. J’y répondrai dès que possible.

A bientôt

PAM

Retrouvez également toutes mes vidéos sur ma chaine YouTube.

Tous les Articles

Le fraisage d’un cube ou parallélépipède rectangle

de

Le 18 février 2023

dans Fraisage

Lorsque l’on doit faire le fraisage d’un cube ou parallélépipède rectangle avec les 6 faces ayant des angles parfaitement droit (90°), il y a une méthode qui permet de garantir que toutes les faces soient alignées perpendiculairement entres elles. Cela s’appelle aussi le cubage d’une pièce.

En priorité, il faut contrôler les alignements de votre table (étau), par rapport a l’axe de la broche. En d’autre terme, votre table doit être le plus plat possible. Sur certaines fraiseuses (fraiseuses universelles), la table est inclinable dans une ou deux dimensions. Si vous n’avez pas de vis de réglage, il faudra caler votre étau à l’aide de clinquants, de manière à ce qu’il soit le plus plat possible.

Première étape

Elle consiste à usiner une première face en serrant la pièce dans l’étau. Une fois fraisée, on indiquera au stylo indélébile « 1 ». On usine uniquement ce qui est nécessaire pour rattraper la surface. Personnellement, je mets quasiment systématiquement un carton entre le mors mobile et la pièce, pour rattraper les erreurs d’alignements entre les deux faces serrées.

Fraisage de la face 1 d'un cube ou parallélépipède rectangle
Deuxième étape

On met en appui la face 1 contre le mors fixe. Attention de garder la pièce dans le même sens. La face verticale qui était à gauche lorsque l’on a fraisé la première face, doit se trouver aussi à gauche. On sert l’étau avec un carton ou un rondin contre le mors mobile. Puis on usine cette face (seulement le nécessaire au rattrapage). On inscrit « 2 ». Si la pièce est petite, le carton suffit, mais il est préférable de mettre un rondin.

Fraisage de la face 2 d'un cube ou parallélépipède rectangle
Troisième étape

On retourne la pièce. On garde la face « 1 » contre le mors fixe et on met la face « 2 » dessous. Puis on sert la pièce avec carton ou rondin, et on usine à la cote voulue. On inscrira « 3 »

Fraisage de la face 3 d'un cube ou parallélépipède rectangle
Quatrième étape

Après on met la face « 3 » contre le mors fixe et la face « 1 » en appuis dessous. On sert sans rondin ou carton et on usine à la cote, la face « 4 ».

Fraisage de la face 4 d'un cube ou parallélépipède rectangle
Cinquième étape

Maintenant on va usiner les deux dernières faces. Pour se faire on met la face « 2 » contre le mors fixe et la face 3 contre l’autre mors, avec une des deux faces non usinée en haut. On usine provisoirement cette face et on y inscrit « 6 ».

Fraisage de la face 6 provisoire d'un cube ou parallélépipède rectangle
Sixième étape

Ensuite on met la face « 1 » contre le mors fixe et la face « 4 » contre le mors mobile avec la face « 6 » en appui dessous et on usine juste ce qu’il faut sur la face « 5 ». On inscrit, ou pas, « 5 ».

Fraisage de la face 5 d'un cube ou parallélépipède rectangle
Dernière étape

Et pour terminer on laisse « 1 » contre le mors fixe et « 4 » contre le mors mobile et on met la face « 5 » en appuis dessous et on usine à la cote la face 6.

Fraisage de la face 6 d'un cube ou parallélépipède rectangle

Il faudra faire attention qu’il n’y ait pas de saletés (copeaux) dans l’étau. De plus, la pièce doit aussi être appuyée correctement au fond de l’étau ou sur la cale, ceci dès que l’appui est sur une face déjà usinée. N’oubliez pas non plus d’ébavurer.

Avec cette méthode de retournement de pièce et appui contre le mors fixe, on garanti les perpendicularités des faces.

Voilà pour le fraisage d’un cube ou parallélépipède rectangle, ce n’est pas très compliqué, il faut juste se souvenir de quelles faces vont où. J’ai préparé ici, un pdf avec les photos, que vous pouvez imprimer et laisser en dessus de votre fraiseuse, comme moi je l’ai fait.

N’hésitez pas à laisser vos commentaires en dessous.

A bientôt

PAM

Retrouvez également toutes mes vidéos sur ma chaine YouTube.

Tous les Articles

Les rapports d’engrenage

de

Le 21 janvier 2023

dans Général

Le calcul d’un rapport d’engrenage est utile lorsque l’on doit faire tourner un axe selon un nombre de tour précis, en rapport avec un autre axe menant. Dans le cas d’un filetage au tour par exemple, il faudra faire tourner la vis mère précisément en rapport au nombre de tour de la pièce. Si vous désirez voir un tuto permettant de calculer le rapport initial (ou total) du train d’engrenage, j’ai réalisé un tuto sur le filetage au tour, ici, qui traite de ce sujet. Ici, nous traitons uniquement la manière d’arriver à ce rapport avec les roues que l’on dispose.

Rappel d’un train d’engrenage

Tout d’abord un bref petit rappel de ce qu’est un train d’engrenage. Vous pouvez avoir un train d’engrenage simple, où il y a que des roues engrenant les unes avec les autres. Comme sur la photo si dessous.

Train d'engrenage simple
Train d’engrenage simple

Dans ce cas le rapport d’engrenage se calcule entre la première roue et la dernière. Les autres roues ne font que d’inverser le sens de rotation, mais en aucun cas ne changent le rapport d’engrenage. Ces roues intermédiaires, sont utilisées, pour permettre de transmettre le mouvement plus loin que ce que l’on pourrait faire avec seulement la première et la dernière.

Ensuite vous pouvez avoir un train d’engrenage avec des roues-pignons comme sur la photo ci-dessous. Une roue-pignon est en fait deux roues montées solidairement sur le même axe. C’est-à-dire qu’elles tournent au même nombre de tour.

Train engrenage avec roue-pignons
Train engrenage avec roue-pignons

Comme les pignons n’ont pas le même nombre de dents que les roues, mais qu’ils tournent à la même vitesse, cela change le rapport d’engrenage. On verra dans les lignes ci- après comment on le calcul. C’est indispensable dans le cas où on n’arrive pas à faire le rapport voulu avec seulement deux roues.

Le calcul du rapport d’engrenage

Passons au calcul :

Le rapport s’écrit toujours en fraction. Ce sera donc

\frac{Z1}{Z2}ou\frac{N1}{N2}ou\frac{Roue~menante}{Roue~menée}

Z indique le nombre de dent

N indique le nombre de tour

Si votre rapport doit être de \frac{1}{2} , cela veut dire que la dernière roue montée sur l’axe mené doit réaliser un demi-tour, pendant que le première roue montée sur l’axe menant fait un tour.

Prenons un premier exemple :

Votre rapport calculé donne 1. Dans ce cas ça s’écrit aussi \frac{1}{1} . Donc vous aurez la première et la dernière roue qui aura le même nombre de dents. SI l’on dispose de deux roues à 50 dents par exemple, alors c’est bon, car \frac{1}{1}~est~aussi~=~\frac{50}{50} .

Maintenant on complique un poil. Le rapport d’engrenage \frac{Z1}{Z2} peut aussi s’écrire :

\frac{Z1}{Z2}*\frac{Z3}{Z4}*\frac{Z5}{Z6}

Le premier engrenage (Z1) correspond toujours au premier engrenage menant.

Le dernier engrenage (ici Z6) correspond au dernier engrenage que l’on doit mener.

Prenons un deuxième exemple :

Votre rapport calculé donne \frac{1}{4} . C’est-à-dire que votre dernier axe mené doit tourner de 0.25 tour pendant que votre premier axe menant, fait un tour.

On inscrit donc sur un papier : Volontairement je mets un « X » pour représenter la multiplication.

\frac{1}{4}=\frac{~~~}{~~~}X\frac{~~~}{~~~}X\frac{~~~}{~~~}

On met autant de fraction que l’on a d’étage disponible dans notre boite d’engrenage. Attention toutefois, si vous devez effectuer une inversion de sens entre la première et la dernière roue. Il vous faudra un nombre d’étage impair, quitte à en utiliser un avec seulement une roue simple.

Le « X » pour la multiplication me permet de savoir quelles roues sont sur quels axes. En fait quelles seront les « roue-pignon », dans mon montage. Il faut vous représenter la barre de fraction comme la dent qui engrène, et la barre oblique (/) du « X » comme l’axe de la « roue-pignon ».

Rapport engrenage montrant les axes des roues-pignons

Avec toutes nos roues dentées que l’on dispose, on doit arriver, en multipliant le haut des fractions, et en multipliant le bas des fractions, à une nouvelle fraction amplifiée de \frac{1}{4}.

\frac{1}{4}=\frac{50}{100}X\frac{50}{100}X\frac{~~~}{~~~}=\frac{2500}{100000}

J’aurai donc la première roue de de 50 dents (Z1) montée sur le premier axe menant (la broche par exemple), qui engrène avec la roue de 100 dents (Z2). Sur le même axe que la roue de 100 dents (Z2), je monte une roue de 50 dents (Z3) et cette dernière roue engrène avec la deuxième roue de 100 dents (Z4) qui est montée sur le dernier axe mené (la vis mère par exemple).

Dans cet exemple, j’ai un étage dans ma boîte que je n’utilise pas.

Toutes les roues que je rajouterai entre deux, fera uniquement inverser le sens de rotation (attention de ne pas rajouter de roue-pignon, mais bien une roue simple).

Montage 0.25 dans une boîte d'engrenage.
Montage 0.25

Sur la photo j’ai ajouté une roue simple de 90 dents, sur le premier étage. Ceci me fait une inversion de sens. Comme je l’ai mentionné plus haut elle ne change pas mon rapport d’engrenage, parce que cette roue est à la fois menée et menante. Je pourrais écrire le rapport comme cela :

\frac{1}{4}=\frac{50}{90}X\frac{90}{100}X\frac{50}{100}=\frac{225000}{900000}

Il peut arriver que l’on ne dispose pas des roues permettant de réaliser le rapport d’engrenage voulu. Dans ce cas, vous aurez deux choix possible. Soit vous êtes outillé pour fabriquer une ou plusieurs roues avec un nombre de dents différents de celles que vous avez, soit vous en achetez et vous adaptez ces roues à votre boite d’engrenage.

En finalité, vous pouvez aussi utiliser cette méthode dans un rapport par poulie. Dans ce cas au lieu d’inscrire Z (qui correspond au nombre de dents), vous inscrirez D (qui correspond au diamètre de la poulie). L’inversion de sens avec une poulie se fait en inversant la courroie et non pas en rajoutant une poulie.

En résumé, la partie la plus compliquée est sans doute de mettre en fraction votre rapport d’engrenage. Vous trouverez ici, un tuto sur les fractions, ou j’explique comment faire. Ensuite ce qui peut être selon les cas un peu long, c’est de trouver les bonnes roues pour votre rapport.

J’espère que cela vous a permis d’y voir plus claire dans ces rapports d’engrenage. N’hésitez pas à laisser vos commentaires en dessous.

A bientôt

PAM

Retrouvez également toutes mes vidéos sur ma chaine YouTube.

Tous les Articles

Fièrement propulsé par WordPress & Thème par Anders Norén