Dans ce tuto, j’essaye d’expliquer la mise en fraction et les manipulations de fractions principales. J’essaye surtout d’amener des solutions toutes prêtes, sans passer par trop de bla bla pour justifier ce que je dis.
Je reviendrai sans doute sur ce tuto par la suite, mais n’hésitez pas à laisser vos commentaires et suggestions en bas.
La mise en fraction d’un nombre décimal.
Exemple ![]()
15 est la partie entière et 678 est la partie décimale.
La partie entière se met en fraction ![]()
![]()
![]()
![]()
![]()
![]()
Donc pour notre exemple on écrira :
![]()
Si ce nombre décimal, comporte une valeur périodique,
Exemple ![]()
Alors on prend les chiffres de la période et on les divise par autant de 9 qu’il y a de chiffre. Pour nous ici, ce sera ![]()
![]()
Il peut aussi arriver que la partie décimale soit avec une partie fixe et une partie périodique.
Exemple ![]()
Dans ce cas on met la partie fixe comme vu plus haut, pour nous ici ce sera ![]()
![]()
Donc on aura :
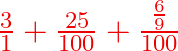
Si le 6 périodique était en 2ème position on aurait eu ![]()
![]()
L’amplification et la réduction de fraction
L’amplification consiste à multiplier le diviseur et le dividende par le même nombre.
Exemple : J’amplifie ![]()
![]()
La réduction de fraction est l’opération inverse. C’est à dire qu’on divise le dividende et le diviseur par le plus grand diviseur commun. Donc dans notre exemple, on peut diviser le haut par 4 et le bas par 4 et on retrouve notre ![]()
La réduction de fraction peut des fois être fastidieuse, lorsque l’on a des grands nombres. C’est pour cela que j’ai mis, ici, un outil qui réduits les fractions.
Cependant on n’a pas toujours accès à ces outils informatique. Une méthode assez rapide pour trouver le plus grand diviseur commun est d’effectuer la division euclidienne (entière) et ensuite de diviser le diviseur par le reste et ainsi de suite jusqu’à avoir un reste égal à 0. Le plus grand diviseur commun est alors le dernier diviseur.
Exemple : ![]()

Le plus grand diviseur commun est donc 1299. Ce qui donne : 5196/1299 = 4 et 6495/1299 = 5
![]()
Attention, l’amplification et la réduction de fraction n’est pas une multiplication respectivement une division de fraction. On verra cela plus bas.
L’addition ou la soustraction de fraction
Il faut tout mettre au même dénominateur commun. C’est à dire qu’il faut avoir toutes les fractions qui ont le même diviseur. On va donc amplifier les fractions et additionner seulement le haut (dividende).
Exemple : ![]()
![]()
On va ensuite réduire cette nouvelle fraction et on obtient.
![]()
Pour la soustraction c’est la même chose, mais ou soustrait au lieu d’additionner.
La multiplication de fraction
Cette opération consiste à multiplier tous les dividendes entre eux et tous les diviseurs entre eux.
Exemple : ![]()
Cela revient au même d’écrire :
![]()
Si on multiplie une fraction par un nombre entier, alors ce nombre entier est aussi ![]()
La division de fraction
Exemple : ![]()
On va prendre le dividende de la fraction du haut et le multiplier par le diviseur de la fraction du bas. Cela deviendra notre nouveau dividende et ensuite on prend le diviseur de la fraction du haut et on le multiplie par le dividende de la fraction du bas et ça devient notre nouveau diviseur. Ceci nous donne donc
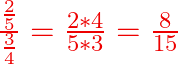
Exemple : ![]()
5 c’est aussi ![]()
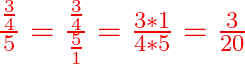
Exemple : ![]()
3 étant aussi ![]()
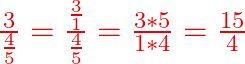
Dans ces deux derniers exemple, on voit qu’il faut faire attention où se trouve le nombre entier. En haut de la fraction principale ou en bas ?
Je reviendrai certainement sur ce tuto concernant les manipulations de fractions, par la suite pour l’améliorer. N’hésitez pas à commenter et me donner d’autres idées.
A bientôt
PAM
Retrouvez également toutes mes vidéos sur ma chaine YouTube.